如何应用SPSS配对样本T检验（SPSS探索测试前后数据的差异）

IBM SPSS Statistics的配对样本T检验与独立样本T检验相似，都可用于对比两个组的均值差异，不同的是，配对样本T检验对比的是两组变量的平均值，计算的是单个个案在两个变量的值的差异，检验其平均差值是否有差异，使用的是变量组的数据。

配对样本T检验适用于同一研究对象测试前、后的均值对比、同一研究对象施于不同方案后的均值对比等。

一、打开数据文件

本文中，我们会以测试初中生饮用牛奶前后身高是否有显著性差异，来演示IBM SPSS Statistics的配对样本T检验的操作方法。

需要注意的是，配对样本T检验使用的是变量组数据。如图1所示，打开两组初中生身高的数据。

图1：身高变量组数据

这两组身高数据有什么区别呢？如图2所示，打开数据的变量视图，为初中生身高A、初中生身高B，两组变量分别标签为饮用牛奶前、饮用牛奶后。

图2：变量标签

二、应用配对样本T检验

接着，依次单击IBM SPSS Statistics的分析-比较平均值-成对样本T检验，打开配对样本T检验功能。

图3：成对（配对）样本T检验功能

如图4所示，在设置面板中，我们可进行多组配对变量的分析，一组配对变量包含两个变量组。接下来，使用实例数据演示操作。

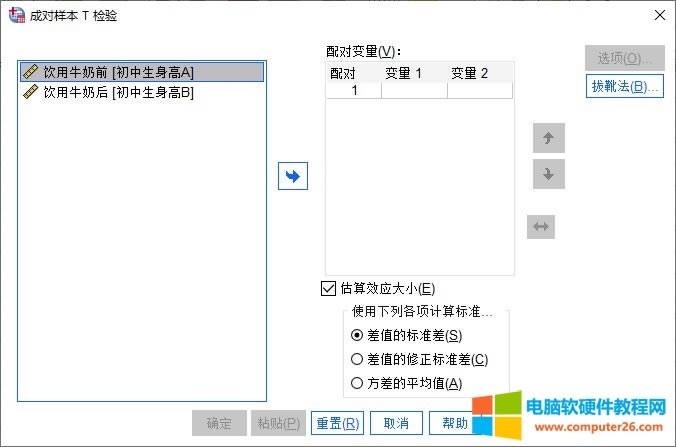
图4：成对（配对）样本T检验功能设置面板

1.选择配对变量

本例中，我们需要探索的是饮用牛奶前后的初中生身高均值是否有显著性差异，因此，可分别将饮用牛奶前、饮用牛奶后的变量配对。

图5：选择配对变量

2.选项设置

接着，针对本例中的数据使用95%置信区间检验差异的显著性，确保较高的准确性。缺失值的处理按照默认的“按具体分析排除个案”选项。

图6：选项设置

3.解读分析结果

完成了以上设置后，运行配对样本T检验，并获得以下分析结果。

首先，先看一下配对样本统计数值，饮用牛奶后的身高均值高于饮用牛奶前的身高均值，但无法确定差异是否有显著性。

图7：配对样本统计

接着，观察配对样本的检验数据，其显著性（双尾）数值接近于0，大于0.05（95%的置信区间），拒绝两变量间无差异的假设，即饮用牛奶后的身高均值显著性高于饮用牛奶前的身高均值。

图8：配对样本检验