如何使用SPSS进行曲线估算区分

回归分析是处理数据、分析数据特征和关系的一种重要方法，在各个领域的数理统计分析中都非常有用。回归分析中有多种分析方法，接下来我们要介绍的是IBM SPSS Statistics中的曲线估算分析方法。

一、曲线估算

和线性回归的原理类似，曲线估算也是以最小二乘法为基础，来分析曲线关系资料在数量变化上的特征和规律的一种回归分析方法。

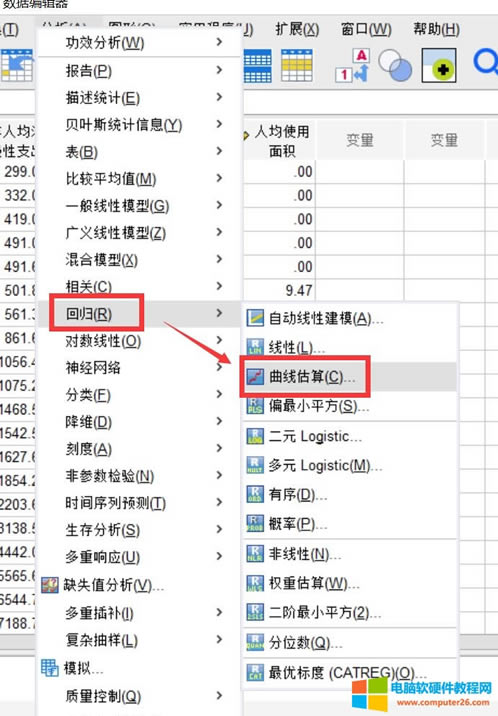
图1：曲线估算

在“分析”菜单中找到“回归”，点击其中的“曲线估算”，可以打开曲线估算的分析窗口。

二、操作方法

1.数据样本

图2：数据样本

这是一份从1978年到2005年某地区人均收入和部分支出情况的统计表，使用曲线估计可以分析年人均可支配收入和教育支出的基本关系。

2.变量设置

图3：变量设置

曲线估计中需要设置三个变量：因变量、自变量和标签变量，我们要探究教育支出随人均可支配收入变化的关系，所以将教育支出移入到因变量窗口内。

自变量的选择要分为两类：时间变量和数字变量，时间变量是一个特例，如果自变量是以时间为刻度变化的，就需要点击选择“独立”中的“时间”，SPSS会自动生成一个时间变量以进行曲线估计。

我们这里使用数字变量即可，点击“变量”，将“人均可支配收入”移入该窗口。

个案标签是用来标记观测距离的变量，将年份移入框内。

3.模型设置

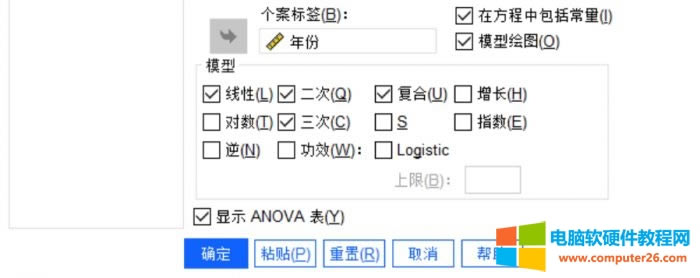
图4：模型设置

我们需要选择一个或多个模型以便于SPSS开始分析，每个模型都是自变量和因变量之间的变化关系，这里选择的是线性、二次、复合和三次。

勾选“在方程中包括常量”、“模型绘图”和“显示ANOVA”表。

4.保存设置

图5：保存设置

这个对话框内可以设置保存的变量类型，包括预测值、残差和预测区间，如果是时间变量，将会激活右侧的预测个案窗口，这里我们不做设置。

5.分析结果

图6：分析结果

在输出日志窗口中，可以看到每个回归模型的分析结果，根据模型的显著性系数小于0.05则该模型显著，可以判断线性、立方和复合模型都是可信的，且三次模型最可信。

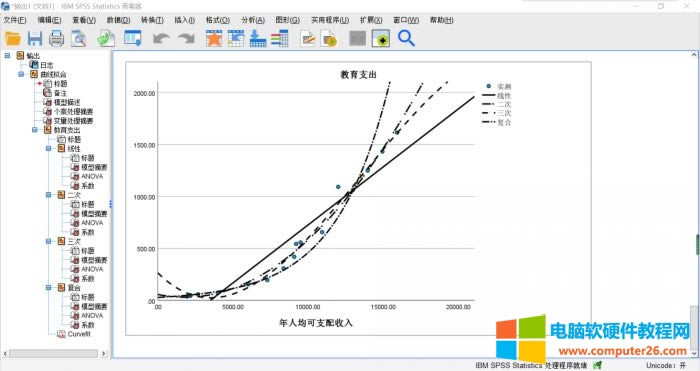
图7：回归图

在分析结果最后，有一个完整的散点图来表示因变量和自变量之间的回归关系，比较观测值和回归曲线、不同的回归曲线，可以分析得出该样本的最佳回归模型是三次模型。

三、小结

本文中我们主要介绍了曲线估计以及如何进行简单的SPSS曲线估算分析，这个方法适用于绝大多数的连续型的数字变量，希望可以对大家有所帮助！